Introduction
Baseball run scoring is collaborative, with offensive success achieved by stringing together hits, walks, steals, and other positive offensive events. The total run production for a player thus depends on that player’s own offensive skill as well as the offensive skill of their teammates. This series considers how to make simple estimates of how a player’s total, context-specific run production depends on their own and their teammates’ inputs.
These estimates have many potential uses. They help us better understand the direct relationship between skill and output. They also help us to better predict the effect of moving a player from one team to another because, when considering a trade, a baseball team should estimate the effect of the change in players on the team’s expected run production.
This article series uses data from the 2021 MLB season to make a simple estimation of the effect of a player’s skill and their teammates’ skill on their total run production as measured by Shapley Run Credits (SRC).
However, before proceeding to our main estimations of interest, we must first take a technical detour to address a statistical concern about different channels by which teammates’ offensive skills may interact. We know that combining good offensive players in a lineup will improve a team’s scoring, and the primary reason for this is that having more strong hitters increases the chance of stringing together sequences of good hitting outcomes that produce runs. We can call this the Sequencing Effect because it refers to the players sequencing together positive batting events without a change in their underlying batting successes.
However, it is also possible that having good offensive teammates can also improve the chances of good batting outcomes of other batters around them. If this is true, then there is an additional effect — which we can call the Spillover Effect — such that a player’s measured batting skill also improves due to having good teammates.
To accurately estimate the effect of teammates on a player’s run production, we must account for both the Sequencing and Spillover Effects if both exist. There is no doubt that the Sequencing Effect exists, so the question is then whether or not there is a Spillover Effect.
Part I of this series investigates whether or not there is an Spillover Effect by estimating whether or not a player’s OPS depends on their teammates’ OPS. If yes, then there is an Spillover Effect such that batting in a lineup with other high-OPS hitters actually increases a player’s own OPS. If no, then there is no Spillover Effect, and the only effect of putting strong hitters together in the lineup is the Sequencing Effect. The analysis will find that there is no statistically meaningful Spillover Effect. With this conclusion, we can proceed confidently in directly estimating just the Sequencing Effect in the subsequent parts of this series.
This part of the series is statistically oriented. Although it is kept at a basic level with raw statistical estimates relegated to the appendix at the end, some readers may want to skip to the Results and Interpretation section below or to Part II.
The Concern
The simple linear equation I ultimately want to estimate is:
SRCperGame = a*OPS + b*TeammatesOPS + constant.
In words, a player’s SRC per game depends on their own OPS, the OPS of their teammates, and some constant term (and a random error term that is left out here and in subsequent equations).
We expect that the coefficients a and b will be positive. A positive a coefficient means that better offensive performance by the player (higher OPS) will increase that player’s SRC per game. A positive b coefficient captures the Sequencing Effect because an increase in the player’s teammates’ OPS should also increase the player’s SRC per game because the player is more likely to be a part of offensive sequences that result in scoring.
If there is only a Sequencing effect, then we can obtain a simple estimate a and b via a linear regression and use the estimated coefficients to predict the change in a player’s overall run production when moving that player from one team to another.
However, if there is a Spillover Effect, then a player’s OPS will depend in part on their teammates’ OPS, and a simple linear regression will yield biased — and hence incorrect — estimates of coefficients a and b. Coefficient a, for example, will actually conflate both the direct of OPS and the indirect effect of the teammates’ OPS through one’s own OPS, thus making the equation fundamentally incorrect. In statistics terminology, having a Spillover Effect implies that both my own OPS and my teammates’ OPS are endogenous variables, in which case the linear regression estimation that assumes that they are not endogenous is fundamentally wrong.
This concern about the Spillover Effect is not unwarranted. A Spillover Effect can exist if batting near other good batters means that hitters will get a higher rate of hittable pitches, or if having more good hitters wears down the opposing team’s pitchers thus worsening their ability to get your team’s hitters out. In each case, the obtains a higher OPS because of having teammates who have high OPS.
The 2SLS Estimation
There is a standard procedure called Two-stage Least Squares (2SLS for short, also called Instrumental-variables (IV) Estimation) for handling endogenous variables. In the first stage of our IV estimation, we estimate an equation that predicts the Teammates OPS using multiple exogenous variables for the player’s OPS and a variable, called the instrument, that is correlated with the players’ Teammates OPS but which would only affect the player’s OPS through its effect on the Teammates’ OPS.
I will here use the teammates’ hard hit rate as the instrument. The argument is that hitting the ball hard is a skill that is not affected directly by one’s teammate. However, having teammates who hit the ball hard causes those teammates to have high OPS and then, if there is a Spillover Effect, increases the player’s OPS. The Spillover Effect, if it exists, must thus operate through the batting outcomes of the teammates.
The first-stage equation to estimate is
TeammatesOPS = c*Speed + d*Contact% + e*HardHit% + f*LineDrive%
+ g*TeammatesHardHit% + constant.
The Speed, Contact%, HardHit%, and LineDrive% variables measures aspects of a player’s batting underlying batting talent, and these are all available from fangraphs.com. TeammatesHardHit% is the hard hit rate of that player’s teammates. Coefficient g is the coefficient of interest, and we want this coefficient to be statistically different from 0 to confirm our assumption that teammates’ hard hit rate is a valid instrument. Coefficients c through f are not of interest.
We then obtain the predicted TeammatesOPS for each player and use them in the second stage regression
OPS = j*Speed + k*Contact% + l*HardHit% + m*LineDrive%
+ n*PredictedTeammatesOPS + constant.
We expect coefficients j through m to all be positive, indicating that having good speed and frequently making contact, hitting the ball hard, and hitting line drives all increase one’s OPS.
However, coefficient n is the key coefficient for us. If is it meaningfully different than 0, then a player’s teammates’ OPS will affect their own OPS, i.e., there is a Spillover Effect. If it is not different from 0, then there is no Spillover Effect.
Results and Interpretation
The full results of the both stages of the 2SLS estimation are presented in the appendix at the end. We here show just the coefficients in the estimated equation for the second stage:
OPS = 0.173*Speed + 0.007*Contact% + 0.010*HardHit% + 0.002*LineDrive%
+ 0.029*PredictedTeammatesOPS – 0.303.
As expected, coefficients j through m are all positive and significantly different from 0 according to standard t tests (their t-statistics as shown in the appendix 5.55, 10.94, 20.86, and 4.05, respectively). In short, having good speed, making frequent contact, hitting the ball hard, and hitting line drives are all causes of high OPS for a player.
However, coefficient n on the predicted teammates’ OPS is not statistically different from 0. Although it is positive (0.029), the coefficient is not meaningfully different from 0 in a statistical sense as evidenced by its very small t-statistic of 0.20.
We therefore conclude that there is no statistically meaningful Spillover Effect because a player’s OPS does not depend on their teammates’ OPS. There will only be the Sequencing Effect.
This conclusion does not imply that a player cannot ever or does not ever help one of their teammates improve. Rather, the conclusion is that there is no such effect that is systematic enough in the data to be accurately estimated, and we can therefore proceed with the rest of our series without concern for the Spillover Effect.
Conclusion
As the first part of a multi-part series, this article investigates whether or not one’s teammates’ OPS affects one’s own OPS. The statistical analysis shows that there is no Spillover Effect, so in subsequent analysis we need to only consider the Sequencing Effect.
Appendix
The analysis combines my SRC data with data on player’s batting downloaded from fangraphs.com. Players who played for more than one team were dropped from the sample. Each regression uses all batters with at least one plate appearance in the 2021 MLB season.
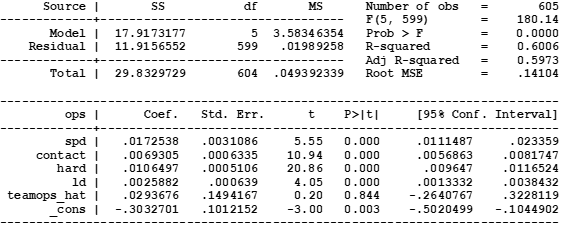
Table A1 shows the results from the first-stage regression of the 2SLS procedure.
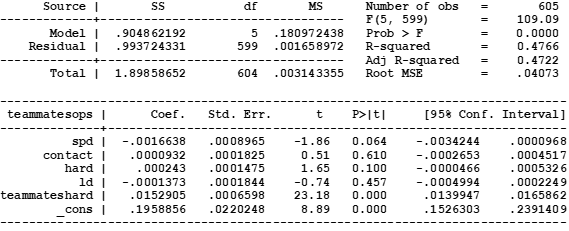
The second-stage regression results are shown in Table A2. Variable teamops_hat is the predicted teammates’ OPS from the first-stage regression above. The coefficient is 0.029 with a t-stat of 0.20, thus indicating that there is no effect of a player’s teammates’ OPS on their own OPS.