Fair-credit Baseball

Introduction

For over a century, baseball box scores have reported runs (R) and runs batted in (RBI) to summarize a player’s contribution toward their team’s scoring. For just as long it has been well known that R and RBI are imperfect measures of players’ run contributions.¹ For example, neither R nor RBI accounts for moving a runner from one base to another who is later batted in, and sometimes a player can bat in a runner without being credited with an RBI. In an attempt to improve upon runs (R) and runs batted in (RBI), Sports Illustrated used Runs Produced — more widely called Runs Participated In (RPI) today — in a series of articles in the 1950s.²

A player’s RPI is calculated as

RPI = R + RBI – HR,

where the subtraction of HR avoids double counting when players bat in themselves. RPI does still appear in various places.³ For example, it is mentioned in various books (e.g., Thorn and Palmer’s The Hidden Game of Baseball⁴), the Baseball Reference web site maintains an entry for Runs Produced, and the Baseball Almanac web site even maintains a career RPI leaderboard.

Yet, the statistic never gained wide traction for two reasons. First, it is still a pretty poor measure of credit for run production, so it did not really succeed in what it set out to accomplish. Second, there was growing interest in measures of skill instead of measures of credit.

This article shows that a modified version of Runs Participated In — which I call Weighted Runs Participated In (wRPI) — improves upon RPI to constitute a simple and easy-to-calculate measure of run production. wRPI is highly correlated with Shapley Run Credits (SRC) over the course of a season, thus making it a viable “shadow stat” for SRC. So, if you do not have a convenient way to calculate SRC, then wRPI serves as a reasonable substitute measure for a player’s overall run contribution.

From RPI to wRPI

As stated earlier, the major problem with RPI as a credit statistic is that it does not always account for when a player participates in a run-scoring coalition but did not receive credit for a R or a RBI. This can happen, for example, when a player advances a runner from one base to another to put them in a position from which they later score. Standard box scores do not contain explicit information about this, so it cannot be included in the calculation.

A second, conceptual problem is that RPI units are somewhat ambiguous. RPI is ostensibly measured in run units, but it is not run units directly. It is more accurate to say that RPI measures how many run-scoring coalitions a player contributed in, be they single-player run-scoring coalitions (i.e., a HR) or multi-player run-scoring coalitions. This is an interesting but atypical way to measure run contributions, and even in this regard RPI is not a perfect measure because it misses the advancing of other runners who score.

We can improve RPI by reconceiving how it accounts for non-RBI run-scoring contributions and by rescaling it run units rather than coalition units. Consider the following calculation of wRPI, which uses different parametric weights than RPI:

wRPI = HR + a*(R – HR) + b*(RBI – HR) +c*X,

where a, b, and c are positive weights (each between 0 and 1) and X are those contributions such as advancing runners that later score but for which no RBI is awarded. X would include sacrifice bunts, fly-ball outs that advance runners from second to third base who later score, etc. This formula says that a player receives a credit of 1 for scoring themselves via a HR, gets fraction a of a run every time they score a run not via their own HR, gets fraction b for every RBI in which they score another player, and gets fraction c for every time they advance a runner who later scores.

Note that X is not accounted for in current box scores, so it is hypothetical integer counting statistics. With X not accounted for in the box score, we have to find a way to use what is available in a box score to construct a proxy for X. Here we assume that advancing runners is highly correlated with (R – HR) and (RBI – HR) because both reflect the player’s success in combining with other teammates to score runs, i.e., getting advanced on base to be advanced by other batters, advancing other runners, and so on. In effect, we assume that a player who is good at scoring runs or batting in runs is also equally good at advancing runners.

To implement this idea formally, suppose that an average non-HR, run-scoring coalition involves three players:  one that is credited with the 1 R, one that is credited with the 1 RBI, and another that is credited with 1 X.  If a player is equally likely to be in either of these three roles in the run-scoring coalition, then a good proxy for X over the course of many games is (R – HR + RBI – HR)/2.

Plugging this expression in for X, we obtain

wRPI = HR + a*(R – HR) + b*(RBI – HR) + c*(R – HR + RBI – HR)/2,

and some simplification yields

wRPI = HR + (a + c/2)*(R – HR) + (b + c/2)*(RBI – HR).

Moreover, if the player is equally likely to be in each of three roles of the run-scoring coalition, then we should should set a = b = c = 1/3.  Plugging in these weights and simplifying yields our final wRPI measure:

wRPI = HR + (1/2)*(R – HR) + (1/2)*(RBI – HR).

That is, wRPI assigns to a player one run worth of credit for each home run (i.e., they get the full credit for scoring themselves), a half of a run of credit for each other run they score, and a half of a run of credit for each run they bat in. Note that the classic, simple RPI = R + RBI – HR is effectively assuming a = 1, b = 1, and c = 0, thereby awarding too much credit for R and RBI and not enough to X. The wRPI weights of a = 1/3, b = 1/3, and c = 1/3 more accurately reflect coalitional run scoring.

To summarize, even though we do not have direct data on X, we can make assumptions about how X is empirically related to R and RBI, use data on R and RBI to estimate X, and then calculate wRPI.

wRPI as a Shadow Statistic for SRC

In assessing the accuracy of different skill estimators, Thorn and Palmer explain that On-base Plus Slugging (OPS) has a remarkably high correlation with their more accurate linear weights method of estimating offensive skill, and this is a very useful fact because OPS is much simpler to calculate.⁵ They concluded that OPS serves as “shadow stat” substitute for their linear weights model when a quick and simple estimate of batting skill is needed. That OPS is such a good proxy for more complex offensive statistics is a main reason why it has gained in popularity in box scores and baseball conversations.

It turns out that wRPI similarly serves as a “shadow stat” for the more accurate but more difficult to calculate SRC. Figure 1(a) plots the season wRPI and season SRC for all 2021 MLB players with at least one plate appearance. wRPI and SRC track remarkably close, fitting closely to the 45-degree line through the origin with a very correlation of 0.971. Because not all runs that score have an associated RBI (e.g., runs that score on groundball double plays), wRPI will slightly underestimate SRC. A linear regression reveals that multiplying wRPI by 1.02 yields the best fit for SRC, so wRPI underestimates SRC by about 2% on average.⁶

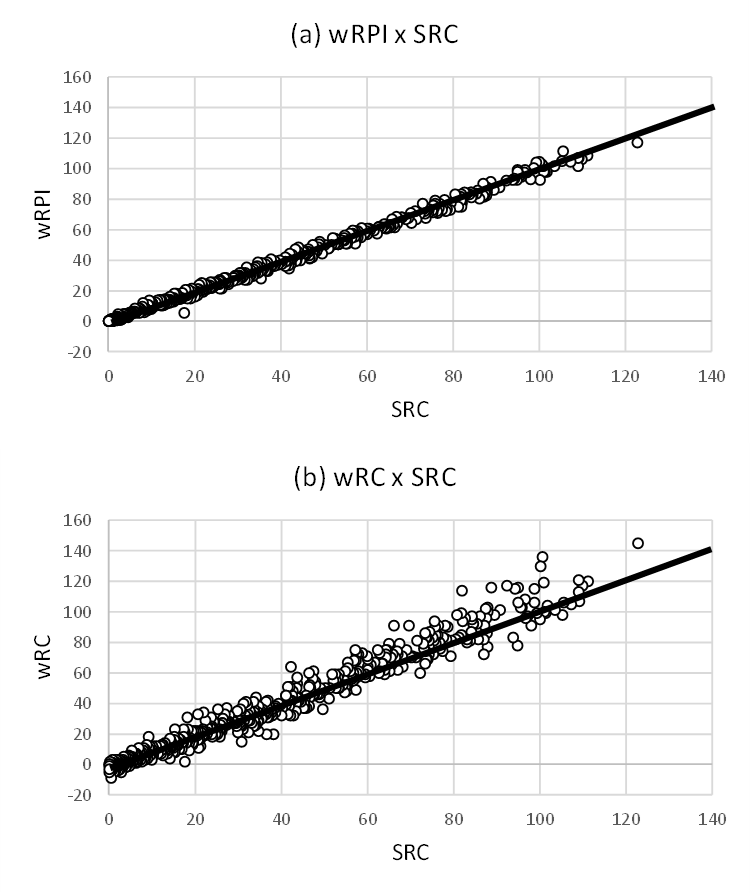
The correlation between wRPI and SRC is tighter than that between SRC and Weighted Runs Created (wRC), which is itself an improved but more sophisticated version of the Runs Created (RC) statistic originally created by Bill James that is meant to estimate a player’s run contributions. Figure 1(b) plots season wRC and SRC for the same 2021 MLB players. The wRC-SRC correlation is still a tight 0.957, but it is clearly worse as seen in Figure 1(b).

To be fair, wRC (and James’s orginal RC) was not meant to be a literal estimate a player’s actual run contributions. Instead, wRC is meant to be an estimate what a particular player’s total run contribution would be on an average team. However, if you are trying to assign credit for what actually happened, then you do not want an estimate of what their contribution would be on an average team; you want a measure of what it would be on their actual team.

SRC is the best method for calculating a player’s run contribution on their actual team, but if SRC is not available, then wRPI is a remarkably good substitute.

Can a More Accurate wRPI be Estimated?

The derivation of wRPI above relied on some strong but reasonable assumptions, one of them being that the a, b, and c weights should each equal 1/3, an assumption that results in the nice and simple weights of 1/2 on (R-HR) and (RBI-HR). However, using linear regression we can estimate the following equation that better predicts SRC:

wRPI = HR + 0.531*(R – HR) + (0.495)*(RBI – HR).

Statistical tests show that the 0.495 coefficient on (RBI-HR) is not statistically different from 0.5 at standard significance levels but that the 0.531 coefficient on (R-HR) is.⁷ Thus, the simple wRPI with the 1/2 weights gives an appropriate weight to RBI but slightly underweights R.

This estimated wRPI provides a better fit, but the overall improvement going from the original, simple wRPI to this estimated wRPI is substantively minor. Linear regressions of the simple wRPI and the estimated wRPI both have R² of 0.99, so the simple wRPI remains a remarkably good shadow stat for SRC.

What About in a Single Inning or Game?

The above analysis compared a player’s wRPI and SRC for a season, but for any particular inning or game there could be a sizeable difference between wRPI and SRC. An example would when a player’s only contribution is to advance a runner who is batted in by another player. This movement of runners will not be accounted for by R or RBI in that particular game, so the wRPI for that player would be 0 while their SRC would be greater than 0.

SRC is the best measure of a player’s actual run contributions in a single inning, game, series, season, or career. Whether or not wRPI is a good estimate for SRC for any particular set of innings or games will ultimately depend on the specifics of the plays in the game. Over the course of a season, however, wRPI provides an imperfect but easy-to-calculate alternative to SRC.

Conclusion

wRPI credits a player with 1 run for every HR, one half of a run for every run scored beyond their HR, and one half of a run for every RBI beyond scoring themselves via HR. Its accuracy in predicting SRC will depend on the particulars of the inning or game, yet if SRC is not available, then wRPI is an imperfect but remarkably good substitute.

Notes

1. See Alan Schwarz, 2004, The Numbers Game: Baseball’s Lifelong Fascination with Statistics, Thomas Dunne Books.
2. See Herm Krabbenhoft, 2009, “Who Invented Runs Produced?,” Baseball Research Journal 38: 135-138.
3. There has been a debate about whether the RPI formula should subtract HR as shown here or not subtract it, but subtracting HR is generally the more-preferred version. See Lee Panas, 2010, Beyond Batting Average: Baseball Statistics for the 21st Century, Lee Panas.
4. Jim Thorn and Pete Palmer, 1984, The Hidden Game of Baseball, Doubleday & Company. New edition published in 2015 by The University of Chicago Press.
5. See pp. 68-69 of Jim Thorn and Pete Palmer, 1984, The Hidden Game of Baseball, Doubleday & Company. New edition published in 2015 by The University of Chicago Press.
6. The linear regression of MLB players’ season SRC on season wRPI yields SRC = 1.0192*wRPI with a very small standard error of 0.002 on the coefficient and a large R² of 0.996.
7. A t-test statistic of 4.39 rejects the null hypothesis that the coefficient on (R-HR) equals 0.5. A t-test statistics of -0.71 cannot reject the null hypothesis that the coefficient on (RBI-HR) equals 0.5.